大気塊の流跡線を計算するMETEXでは、大気塊の位置の時間変化を気象データを使って算出します。以下の手順で、気象データの時間・空間補間と、大気塊の動きを推定するための時間積分を繰り返し行います。
- 初期条件となる緯度、経度、高度、時刻を指定
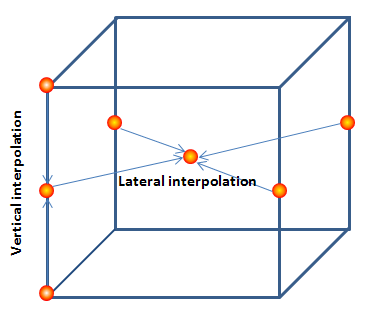
- 指定した時刻の前後にある気象データを読み込み、指定した位置(緯度、経度、高度)を囲む3次元格子を求める
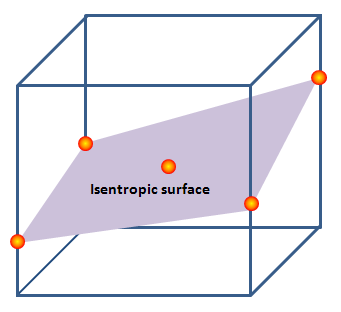
- 2つの時刻の気象データに関して、指定した位置での気象値を3次元格子の8つの頂点を用いて空間的に補間
- 空間補間された2つの時刻の気象値を時間的に補間することで、指定した時刻における大気塊の位置での気象値を求める
- 4で求めた時刻・位置における風速を用いて積分のタイムステップを推定
- 指定した移動経路算出モデルに従い、積分解法によりタイムステップ経過後の大気塊の新しい位置を求める
- 2~6を指定された期間繰り返す